MATEMÁTICAMENTE LA MITAD DE 85 dB ES 82 dB, VEA LA EXPLICACIÓN

 Por Eric Omaña

 

 La mitad de 85 decibeles, es decir, 85/2 dB = 82 dB. Esto es solo valedero en operaciones logarítmicas. ¿Pero que tiene de importancia esto? Bueno resulta que en la cabeza de casi todo el mundo que hace prevención de los peligros y amenazas presentes en los lugares de trabajo, así como el análisis de los riesgos, está en recurrir al equipo de protección auditiva por encima de 85 dB, pero resulta que el Artículo 68 de la LOPCYMAT demanda recurrir a la protección del personal, ya sea en forma colectiva, en este caso, colocando a la gente en un ambiente isonorizado o aislando la fuente sonora, o  con protectores auditivos, cuando se supera el 50%, es decir, la mitad del nivel técnico de referencia considerado seguro.

 Por eso en este mundo todo es relativo y cada vez que queremos hablar o conocer de algo tenemos que contextualizar, conceptualizar, revisar la historia, en fin, ir al conocimiento holístico, porque la formación que hemos recibido hasta ahora, basada en los modelos positivistas nos hace dependientes, coartando la capacidad de la innovación y despojándonos en consecuencia de la esencia humana, que debe poner en duda todo para ir a la raíz de las cosas.

Con las siguientes explicaciones matemáticas al problema de porqué la mitad de 85 dB es exactamente 82 dB cumplimos lo ofertado en el curso en línea que dictamos, los colegas Rimsky Materán y Eric Omaña, sobre el tema ruido, y como escribimos en el chat de AVHORenacer, la clave está en que log 2 = 0,3

Hemos planteado para el conversatorio que hicimos de Control Técnico de Ruido que se diera explicación matemática de porque 82 dB representan la mitad de 85 dB, valor que de acuerdo al Art. 68 de la LOPCYMAT, demanda del empleador “iniciar acciones de control” y ofrecimos la respuesta en este blog. Bueno ahí les va.

  UNA EXPLICACIÓN MATEMÁTICA

Partamos de NPS = 10 log (P/Po)²  con Po = 2x10^-5 Pascal 

donde NPS es el Nivel de Presión Sonora, Po es la presión de referencia, aquella a la que se detecta el ruido por primera vez, en una escala de ascenso, propio de un oído completamente sano, y P es la Presión que genera el fenómeno que estemos evaluando.

Si NPS = 85 despejamos la presión P para manipular pascales, que lo puedo hacer aritméticamente, vean que el 10 pasará de multiplicador a divisor, además se conoce el valor de Po

La ecuación quedaría así, inicialmente:

85 = 10 log (P/Po)²

85/10 = log (P/Po) ² elevamos ambos lados de la ecuación a la potencia base 10 y queda
10^85/10 = P²/Po² eliminando así la expresión log

10^8,5 = (P/Po)²

ordenemos la ecuación para visualizarla mejor: (P/Po)² = 10^8,5
luego despejo P, es decir, vamos buscando la presión que es producida por el fenómeno en estudio, recordando que  Po=2x10^-5

P² = ( 10^8,5) (Po²) = ( 10^8,5) (2x10^-5)² = ( 10^8,5)(4)(10^-10)

P² = 4x10^(-1,5)

Pe² = 0,127 A ESTE VALOR SE LE OBTIENE LA MITAD (50% PASCALES)

NUEVO P²=0,0635 valor que insertamos para determinar el nuevo NPS, Lp o como lo quieran llamar, usaré LP

Lp = 10log(0,0635/4x10^-10)

Lp = 10 log (1,59x10⁸)
Lp = 10 (log 1,59 + 8 log 10)
Lp = 10 (0,2 + 8) = 82

Así Lp 50% es 82.

Como decían mis profesores LQQD.

Si se usa Lp = 20 log (P/Po) da igual solo que al despejar P para conseguir el 50% deben elevar el resultado al cuadrado

La explicación de esto se deriva de la relación entre la Intensidad sonora y la fluctuación de presión del aire, I=P²/dc, donde I es intensidad, P es la presión media cuadrática, d es densidad del aire y c es la velocidad del aire.

OTRA EXPLICACIÓN MATEMÁTICA

Leonor Ángeles Hernández <leonor.angeles1@gmail.com> , cursante de la Especialización de Higiene Ocupacional en la Universidad Bolivariana de Venezuela (UBV) lo resolvió usando el concepto de Intensidad Sonora así:

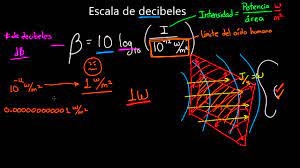
La ecuación matemática para determinar la intensidad del sonido en decibelios (dB) es la siguiente:

dB = 10[ log (I / Io)]
donde I es la Intensidad de sonido que emite una fuente particular, Io es la Intensidad minima auditiva para el ser humano; la cual tiene un valor constante de Io = 1x10^-12 W/m2.
Aplicando propiedades de los logaritmos y sustituyendo el valor de Io, la ecuacion queda:

dB = 10[ log (I / 1x10^-12)]

dB = 10log I – 10log( 1x10^-12)
dB = 10log I – [10log 1 + 10 log (10^-12)]
dB = 10log + 120
Si la intensidad en decibelios es dB = 85, buscamos cuanto es la intensidad en unidades de W/m2 despejando I

85 = 120 + 10log I
85 - 120 = 10log I
-35 = 10log I
-3,5 = log I ; al aplicar antilogaritmo, el valor de I = 0,000316 W/m2.

Luego, si se aplica el mismo procedimiento para una intensidad en decibelios de dB = 82:
82 = 120 + 10log I
82 - 120 = 10log I
-38 = 10log I
-3,8 = log I ; al aplicar antilogaritmo, el valor de I = 0,000158 W/m2.

Entonces 0,000158 x 2 = 0,000316, por lo que la intensidad de sonido de 82 dB es, matemáticamente y en unidades de W/m2, la mitad de la intensidad correspondiente a 85 dB.

HAY OTRAS EXPLICACIONES, PUEDE UD. INIDICARLAS?